Momentum torquens est vis torquens quae rem rotare facit. Cum ianuam aperis aut cochleam torques, vis quam applicas multiplicata per distantiam a puncto cardinis momentum torquens creat.
Cardinibus, momentum torquens vim rotationis a operculo vel ianua gravitate generatam repraesentat. Simpliciter dictum: Quo gravius operculum et quo longius eius centrum gravitatis a cardine est, eo maior momentum torquens.
Intellegentia momenti torquendi adiuvat te cardinem rectum eligere ne tabula cedat, subito cadat, aut nimis levis sentiatur dum clauditur.
Cur Momentum Cardinis Calculandum Est?
Cardines late in operculis versatilibus et structuris armariorum adhibentur. Exempla includunt:
● Ecrana computatralia portatilia – Cardo vim torquentem sufficientem praebere debet ad pondus ecrani aequandum.
● Opercula arcae instrumentorum vel armariorum – Haec saepe latiora et graviora sunt, maiorem torquendi vim efficientes.
● Ostia instrumentorum industrialium vel opercula instrumentorum – Tabulae graves cardines satis firmos requirunt ne casus inopinatus fiat.
Si vis torquens nimis parva est, operculum subito claudetur.
Si torques nimis altus est, operculum difficile aperitur aut rigidum sentitur.
Computatio momenti torsionis cardinis efficit ut momentum torsionis cardinis maius sit quam momentum ab operculo generatum, unde usus lenis et tuta fit.
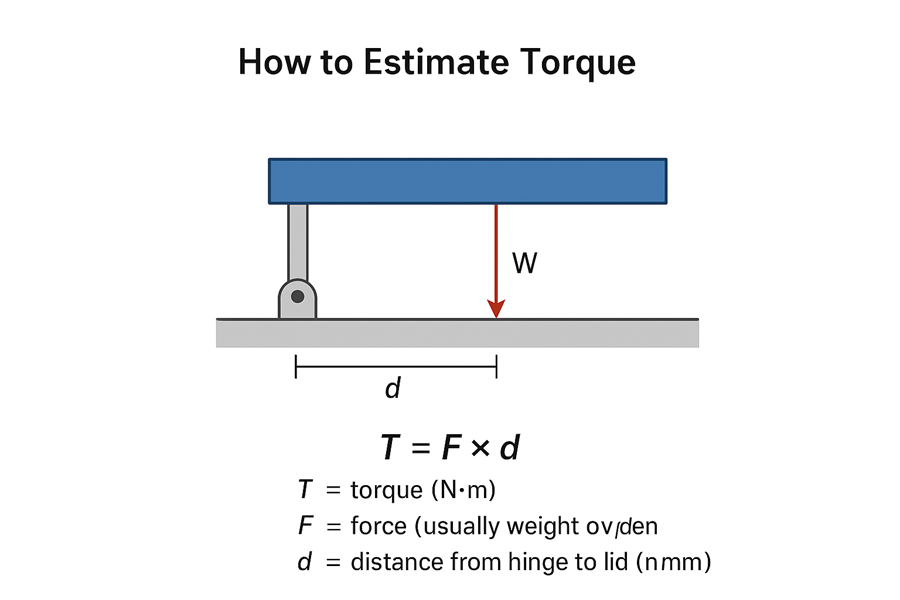
Quomodo Momentum Torquens Aestimare
Principium fundamentale est: Momentum torquens = Vis × Distantia.
Formula est:
T = F × d
Ubi:
T= momentum torquens (N·m)
F= vis (plerumque pondus operculi), in Newtoniis
d= distantia a cardine ad centrum gravitatis operculi (distantia horizontalis)
Ad vim computandam:
F = W × 9.8
(W = massa in kg; 9.8 N/kg = acceleratio gravitatis)
Pro operculo uniformiter distributo, centrum gravitatis in medio puncto (L/2 a cardine) situm est.
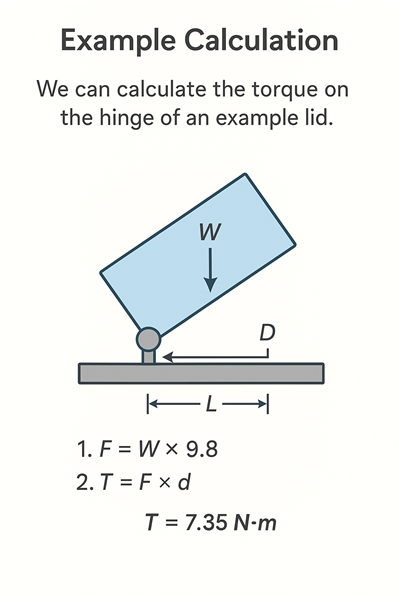
Exemplum Computationis
Longitudo operculi L = 0.50 m
Pondus W = 3 kg
Distantia centri gravitatis d = L/2 = 0.25 m
Gradus 1:
F = 3 kg × 9.8 N/kg = 29.4 N
Gradus 2:
T = 29.4 N × 0.25 m = 7.35 N·m
Hoc significat systema cardinis circiter 7.35 N·m momenti torquendi praebere debere ut pondus operculi compenset.
Si duobus cardinibus uteris, uterque cardo circiter dimidium momenti torsionis fert.
Conclusio
Ad momentum torsionis cardinis requisitum aestimandum:
● Momentum Momentum (T) = Vis (F) × Spatium (d)
● Vis ex pondere operculi venit.
● Distantia a centro gravitatis determinatur.
● Duo cardines onus torquens dividunt
● Semper cardinem elige cuius torques paulo altior quam valor computatus est.
Supradicta tantum principia fundamentalia sunt. In applicationibus realibus, factores additionales etiam considerandi sunt cum momentum torsionis cardinis calculatur. Libenter nobiscum communicare potes, et simul proiectum tuum accurate examinare poterimus!
Tempus publicationis: XVII Kalendas Ianuarias, MMXXXV









